Difference Between Squirrel Cage And Wound Rotor Induction Motor Pdf
Contents • • • • • • • • • • • • Introduction There are two main types of induction motors exists. They are, • Squirrel cage induction motor • slip ring induction motor In previous, we saw complete details related to slip ring induction motor. Here we know the fundamental details related to squirrel cage motor. What is squirrel cage induction motor?
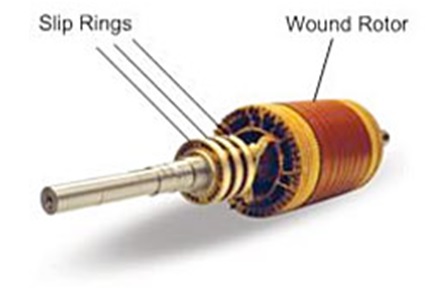
A wound rotor induction motor has a stator like the squirrel cage induction motor, but a rotor with insulated windings brought out via slip rings and brushes. Parts of an Induction Motor. An induction motor has 2 main parts; the Stator and Rotor.
In simple words, the induction motor which uses a squirrel cage rotor is called squirrel cage induction motor. The reason behind the name “squirrel cage” is because of the type of rotor used in these motors. In these type of motors, the rotor is simplest and most rugged in construction.
This is the NES emulator for the Nintendo DS. I have included the full USA NES romset in with this emulator, over 1000 roms. When you extract the rar file, you will have a single folder named NES. Download Best NES ROM Pack! • Full Rom Sets @ The Iso Zone • The Ultimate Retro Gaming Resource. Nes roms complete torrent.
These motors have much higher efficiency than slip ring induction motors. Most of the industries prefer these type of motor due to less maintenance cost, higher efficiency, and their lightweight construction. Let see the construction of squirrel cage induction motor. Squirrel cage induction motor construction Any Induction Motor has main two parts: a Stator and a Rotor. The construction of of the induction motor is almost the same as other motors. But the rotor construction differs with respect to the type of motor.
Slip ring induction motor is made up from and squirrel cage induction motor is made up from the squirrel cage rotor. Stator The stator is the outer component of the motor which can be seen. A stator is in all the motor only winding on the stator is vary with types of motor. In squirrel cage induction motor, there is a 3 phase winding on the stator slots.
Windings are such placed that they are electrically and mechanically 120 o apart from in space. These windings are either star connected or in delta connected.
The winding on a stator is mounted in such a way that it provides low reluctance path for generated flux by A.C current. The insulation between the windings is generally varnish or oxide coated. Now let’s move toward the construction of the squirrel cage rotor.
Squirrel cage Rotor Almost 90% of induction motors are provided with a squirrel cage rotor because of its very simple, robust and almost instructible construction. In this type of motor, the rotor is cylindrical core which is laminated to avoid power losses. Squirrel cage rotor is made up of aluminum or copper bars which are placed parallel to each other and all the bars ( conductors ) are short-circuited with end rings. The rotor conductors and end rings form a complete closed circuit. Here rotor core is laminated to avoid power losses from eddy current and hysteresis. In motor rating up to 100 kW, the squirrel cage rotor is made up from the aluminum cast. In this type of rotor, conductor bars and end rings are permanently short-circuited so we can’t connect any external resistance in rotor circuit for starting purpose.
In previous, we saw we can add external resistance in the rotor in slip ring induction motor. Other parts of motor: A fan is attached to the back side of the rotor to provide heat exchange, and hence it maintains the temperature of the motor under a limit. Bearings are provided as the base for rotor motion, and the bearings keep the smooth rotation of the motor. In other, starter is also provided with the motor for limiting the starting current. For effective starting of induction motor different methods are used. Check this- now let’s see how squirrel cage induction motor works?
Activation code windows xp. Manual 3ds Max 2012 Keygen Xforce 64bits.
Let see squirrel cage induction motor working principle below. Squirrel cage induction motor working principle In D.C motors we need to give supply to stator and rotor both for excitation. But here in the induction motor, we only need to give supply to the stator winding for operation. Actually what happens let’s see. Actually, when we give supply to stator winding then the current starts to flow in the coil will produce a magnetic flux in the coil. Now, here the rotor windings are short-circuited. Induced flux from the stator winding will cut the coils in the rotor, and As the Faraday’s law of electromagnetic induction will cause the current to flow in the coil of the rotor due to the short circuit of the rotor coil.